RIDGE

Rhombus diagonal problem

[ Description ] [ Prior knowledge ] [ Possible learning ] [ Solutions ] [RIDGE Home] [ RIDGE Problems ]

Description:

Source(s):

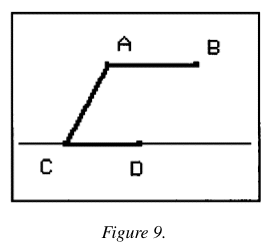
Construct a shape (Figure 9) fitting the following conditions:

1. Segment AB is parallel to segment CD (i. e., AB // CD).

2. Segment AB has the same length as segment AC (i. e., AB = AC).

fig 9

Construct segment CB (Figure 10).

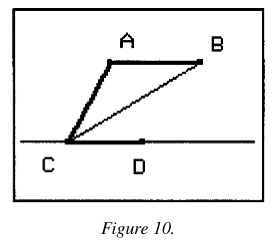
fig 10

Investigate: Is segment CB the angle bisector of angle ACD?

Justify your affirmative or negative answer to previous question. We assume that your conclusion is true, but why is it true? It is necessary to use geometric properties studied and accepted in the classroom.

Marrades R., Gutiérrez Á. 2000

[Top]

Prior knowledge

Prior DGS content required:

None. Can be done with pencil and paper.

Prior mathematical content required:

Isosceles triangle properties.
Parallel line properties.

Prior mathematical content related:

Diagonal properties of quadrilaterals

[Top]

Possible learning

Likely mathematical content learned:

Diagonal properties of rhombus

Likely DGS content learned:

Angle measure
Angle bisector

[Top]

Possible solutions

To discover that the segment CB is the angle bisector of angle ACD might be done by experiment in a dynamic geometry environment or a pencil and paper environment.

To prove that it is can be done by observing that triangle ABC is isosceles, and so angle ACB is congruent to angle ABC. Angles ABC and BCD are also congruent because they are alternate interior angles of a transversal of two parallel lines. Therefore angles ACB and BCD are congruent and so CB bisects angle ACD.