|
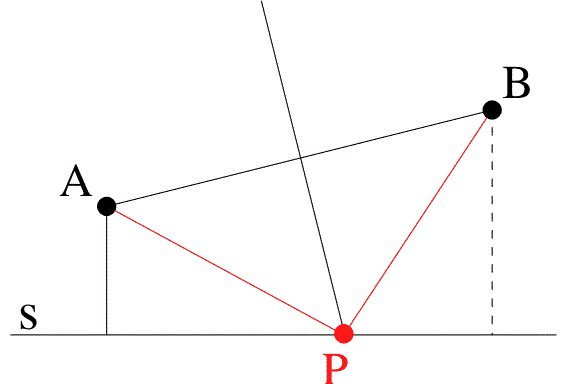
Consider the diagram
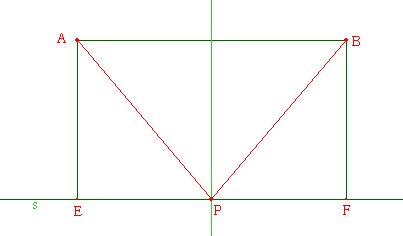
shown in Figure 4a. In this special case the
position of P is in the centre, which suggests Conjecture 2:
P is the
intersection between s and the perpendicular bisector of AB. (see
Figure 4).
[We have retained the
numbering of the conjectures used by
Figueiras
& Deulofeu (2005) but we believe this conjecture to be the
beginning of a discovery process.]
|
Figure
4
|
|
It is possible that
those who made conjecture 2 used their
knowledge that the perpendicular bisector is the locus of
equidistance
between two points. Why this particular knowledge was active
for these
students is not clear (Perhaps they had solved a problem in which it
was important recently??). But it is reasonable to
make use of this
knowledge. They are considering a path made up of
two parts AP and
PB. Not knowing how to minimise the total distance
they might have
considered the easier problem of minimising the longer part.
If the
total distance were fixed then the longer part is minimal
when the two
arts are equal, which occurs when P lies on the perpendicular
bisector
of AB (see Figure 4).
|
Figure
4a
|
|
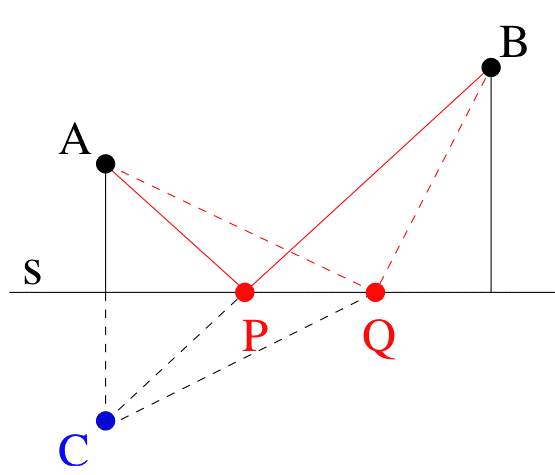
Unfortunately, the total
distance is not fixed
(as we are trying to minimise it) so the reasoning is flawed
and a
counter example can be found, when the horizontal distance
between A
and B is small compared to the vertical distance between them
(see
Figure 5). Conjectures 2 & 3 illustrate an
interesting confusion
that occurs in solving such problems: equal distances are
often confused with shortest distances. Knipping (2005)
discusses a similar confusion in another minimum distance
problem, finding the point such that the total distance to
the sides is minimal (the Beach Problem). Their initial conjecture was the
centre of the incircle. This diagram (Figure 5) in the context
of the reasoning that has gone before, suggests the next
conjecture:
Conjecture 3: P is the
intersection between s and its perpendicular through the
mid-point of AB. (see Figure 5).
The problem it reveals is
that the point P should stay on the segment ED that is the
projection of AB onto s. This constraint, combined
with the earlier consideration of trying to equalise
distances, suggests that the midpoint of ED, or alternately
the projection of the midpoint of AB onto s, is the point P.
This new construction also accounts for the known special
case shown in Figure 4a.
|
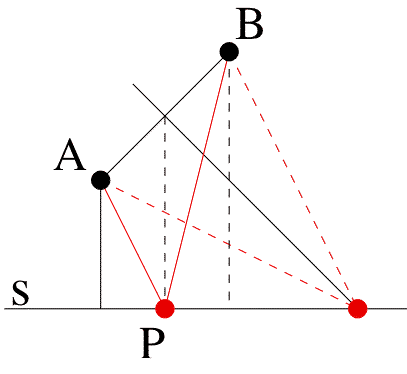
Figure 5 |
|
If A is on s, however, a
new counterexample is produced (Figure 5a).
This diagram shows clearly the correct solution in another
specific
case: When A is on s then the shortest path is AB itself. The
emphasis
shifts to defining P is such a way that it can be seen as a
continuous transformation from this initial situation. As A
moves up,
P must move to the right.
|
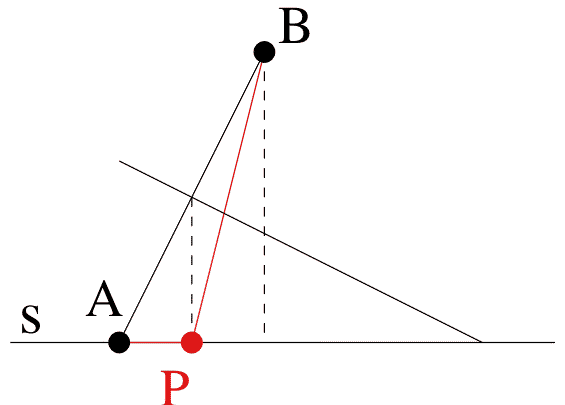
Figure 5a |
|
The segment EB provides
a mechanism to
produce this motion: A is projected horizontally onto EB to
the point
O and then O is projected vertically onto s to the point P
(Figure 6). This gives rise to:
Conjecture 4: r is the
perpendicular to BD
through A; O the intersection of r and BE; and P the
intersection between s and its perpendicular through O. (see
Figure 6).
|
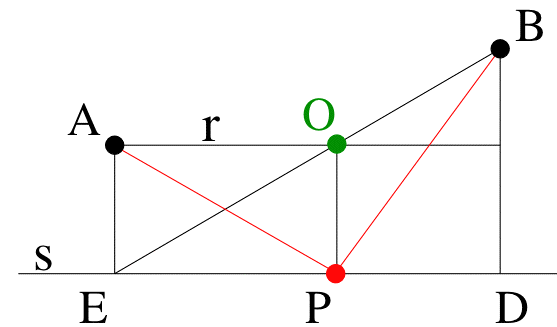
Figure 6 |
|
Again a counter-example
is not hard to find (Figure
6a),
because this
construction does not work in the original special case, when
EA=DB.
|
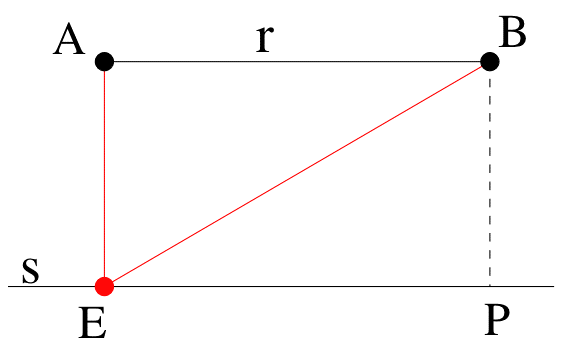
Figure 6a |
|
Combining the two
special cases (and the mirror image of
the
second)
produces the diagram shown in Figure 7a, which immediately
suggests:
|
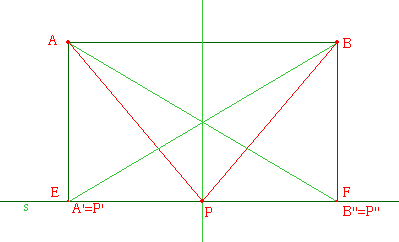
Figure
7a
|
|
Conjecture 5: O is the
intersection between AD and BE.
P is
the
intersection between s and its perpendicular through O (see
Figure
7).
Thus through a sequence
of conjectures, each one based on
a
single special case (except the last which is based on two
special
cases), a conjecture is produced that turns out to be
correct.
|
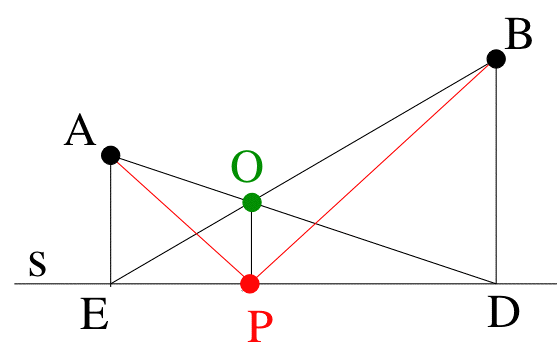
Figure 7 |