previous table of contents next
Section I
The study of the learning of proof in schools is a significant field in
current research in mathematics education.
The field has progressed from studies indicating that students have
difficulty with proof (Senk, 1985; Fischbein, 1982) to studies of small groups
engaged in proving (Reid, 1995a; de Villiers, 1992), philosophical
considerations (Hanna, 1983) and ethnographies of current classroom practice (Schoenfeld,
1988; Sekiguchi, 1991).
The study of the learning of proof takes place within a larger field of
enquiry into reasoning, which has lately received increasing emphasis in
mathematics education research (e.g., Stiff, 1999) This report describes the
result of one phase of the Psychology of Reasoning In School Mathematics
(PRISM)*
project, in which a teaching experiment model was used to add to our
understanding of students’ use of the reasoning that underlies proof.
The main objective of the PRISM project is to continue the development of a model (first described in Reid, 1995a) for describing students’ reasoning that includes needs. This model is intended to be applicable to the description of mathematical reasoning at every level of schooling. It distinguishes among individuals’ degrees of formulation of deductive reasoning, styles of reasoning, and needs related to reasoning (especially explaining, exploring and verifying). “Needs” in this model describes the student’s goals or purposes in reasoning in a particular way and context. Deductive reasoning has been identified by the
The
Psychology of Students' Reasoning in School Mathematics
David A Reid
Page I-1
To Beginning of Section | To End of Section
National Council of Teachers of
Mathematics (NCTM, 1989), the Cockcroft Report (1982) and other calls for
reform in mathematics teaching as an area of central importance to mathematics
instruction. Research in this area contributes directly to the psychology of
mathematics education, and has implications for the current reform of
mathematics teaching and learning in both primary and secondary schools.
Three specific questions are being investigated in the PRISM project:
1.
In what ways can the mathematical reasoning of primary school students
and the needs associated with their reasoning differ from those of secondary
school students?
2.
How can teaching interventions and other features of learning
mathematics in schools foster emotional orientations toward reasoning and
create occasions for deductive reasoning and the formulating of that
reasoning?
3.
To what extent do the models of needs to reason developed in previous
research describe students’ reasoning at various school levels, and how
might they be improved?
The first question addresses the need for research that bridges the divide between research done with young students and research at the secondary and post-secondary level. Work at the primary level has shown that young children can reason in sophisticated ways (English, 1996; Zack, 1995, 1997; Graves & Zack, 1996; Maher & Martino, 1996; Lampert 1990). Research on deductive reasoning at the secondary level, however, suggests that students are not able to
* This research project has been funded by Social Sciences and Humanities Research Council of Canada grant #410-98-0085, and by internal grants from Memorial University and Acadia University.
The
Psychology of Students' Reasoning in School Mathematics
David A Reid
Page I-2
To Beginning of Section | To End of Section
apply their reasoning when called to do so in formal
mathematical contexts (Fischbein, 1982; Senk, 1985).
In the PRISM project the same model for reasoning is being used to
describe the reasoning of students at a wide range of grade levels allowing
comparisons to be made that may provide insight into the development of
mathematical reasoning from primary to secondary school.
The research reported here provides background for future research into
this question, but does not address it directly.
The second question addresses the extent to which it is possible to
create occasions for deductive reasoning while working within the constraints
of existing provincial curricula and the aims of reform documents, such as the
Curriculum and Evaluation Standards
and Professional Standards for Teaching
Mathematics (NCTM 1989, 1991). This
question is ultimately tied to a long term goal of offering researchers and
teachers examples of teaching in which deductive reasoning was encouraged, and
providing materials that will assist them in fostering such occasions in their
own classrooms. In the grade 2
contexts games were used as the primary contexts for study. Result relevant to this question will be discussed in Section
III.
The third question is concerned with the feasibility of understanding the
deductive reasoning of younger students using existing models.
Can characteristics of the development of deductive reasoning in
primary school students be described using models for describing the reasoning
of secondary school students? Investigations
of this question will produce improved models for examining mathematical
reasoning at all levels. The
research reported here addresses the reasoning of younger students, and
modifications to the model resulting from this research will be discussed in
Section III.
The
Psychology of Students' Reasoning in School Mathematics
David A Reid
Page I-3
To Beginning of Section | To End of Section
Previous
research on deductive reasoning.
Research into deductive reasoning in mathematics has been conducted from
several different perspectives. The
considerable body of research into logic and mathematical proof, conducted
especially in connection with the New Math reforms, contains much that is
relevant. A smaller body of
research (Reid, 1995a; de Villiers, 1992; Bell, 1976) exists that is concerned
directly with the nature of deductive reasoning in mathematics, and the needs
that reasoning can satisfy. There
also exist several research projects directly concerned with mathematical
reasoning in school contexts.
The main conclusion of previous research on deductive reasoning is that
most students do not understand the nature of proof (e.g., Fischbein, 1982;
Senk, 1985) and do not reason logically in many situations (Henle, 1962; Wason,
1966). Large scale studies in the
United States have found that most students (e.g., 70% in Senk, 1985) do not
understand the proofs they study in high school geometry.
Other studies have indicated that students are confused about the
relationship between examples and proofs (Alibert, 1988; Bell, 1976; Chazan,
1993; de Villiers, 1992; Finlow-Bates, 1994; Fischbein, 1982).
Other researchers (Balacheff, 1991; Braconne & Dionne, 1987;
Schoenfeld, 1988; Shanny & Erlich, 1992) have found that both students and
teachers concentrate much more on the appearance of proofs than on their
logical content. This focus contributes to problems in understanding proof (Schoenfeld,
1988).
The
Psychology of Students' Reasoning in School Mathematics
David A Reid
Page I-4
To Beginning of Section | To End of Section
Most of the research on proof mentioned above does not consider students’
emotional orientations to be important to their reasoning.
There is an implicit assumption that the need of many mathematicians to
use deductive reasoning to verify mathematical statements is shared by
secondary school students. Research by Reid (1995a), building on the
psychological studies of de Villiers (1991) and Bell (1976), indicates that
students often use deductive reasoning to explore and explain mathematical
phenomena, suggesting that an emotional orientation to satisfy a need to
explain or explore through deductive reasoning is already present in some
secondary students. The
assumption that students have an emotional orientation toward using deductive
reasoning to satisfy a need to verify may be at the root of students’ poor
understanding of proofs and other topics related to deductive reasoning.
Work in the philosophy and sociology of mathematics by Hanna (1983),
Tymoczko (1986), Lakatos (1976), and others, shows that the use of deduction
to explore and explain is also widespread among professional mathematicians,
suggesting that the concept of mathematical proof at the post-secondary level
could be developed from the emotional orientations secondary school students
already have.
The PRISM project is be a continuation of a program of research into students’ reasoning processes begun by Reid in 1990. Initial research into university students’ understanding of proof by mathematical induction (Reid, 1992) revealed the importance of formulation in students’ reasoning, especially in the development of informal or everyday reasoning into mathematical proving (Reid, 1993). It also suggested that the needs students had for reasoning deductively had significant implications for the development of mathematical reasoning. More recently a study of the needs deductive reasoning satisfies for high school and university students and the contexts in which these needs arise has
The
Psychology of Students' Reasoning in School Mathematics
David A Reid
Page I-5
To Beginning of Section | To End of Section
revealed the
importance of exploring and explaining as needs for reasoning deductively
(Reid 1994a, b, 1995a, b, c). This
research into the psychology of mathematical reasoning has provided a basis
for developing the PRISM project, which seeks to investigate whether these
results are applicable in schools.
The model developed in earlier research addresses four aspects of
reasoning: needs; types; formulation; and formality. In the PRISM project, special attention is being paid to
elaborating on needs and formulation.
Needs are the purposes or goals of reasoning. Explaining, exploring and verification are the main needs
identified in the current model.
Types of reasoning covered are: deductive (reasoning from general
principles); inductive (the generalization of specific cases); and analogical
(reasoning by similarities). These
three types are suggested by Pólya (1968). Two
other types, abductive reasoning and generalizing, have been added as a result
of research done since the model was first developed.
Formulation applies chiefly to deductive reasoning.
It describes the extent to which the reasoner is aware of her or his
own reasoning. It also includes
reasoning that is automatic (e.g., the use of algebra) or superficial (i.e.,
it has the appropriate form, but the underlying understanding is absent).
Formality applies only to written deductive proofs, and categorises them according to their adherence to mathematical norms for the presentation of reasoning.
The
Psychology of Students' Reasoning in School Mathematics
David A Reid
Page I-6
To Beginning of Section | To End of Section
These categories are linked by paths which indicate combinations which
have been observed in past research. Figure
1 (from Reid, 1995a) shows the model as it was first proposed.
Table 1 lists subtypes of the need to explain derived from work at the
grade 10 research site. Section
III contains additions based on the research reported here.
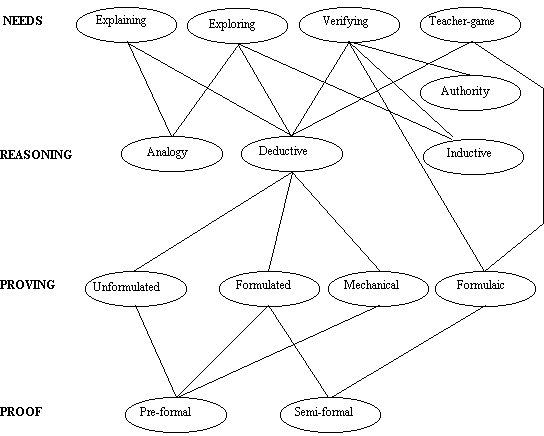
Figure 1:
The Model presented in Reid 1995
The
Psychology of Students' Reasoning in School Mathematics
David A Reid
Page I-7
To Beginning of Section | To End of Section
|
E: Explaining to someone else |
EH: Explaining how |
EHT: Explaining how prompted by
a teacher or written prompt EHN: Explaining how not prompted by a teacher or written prompt. |
|
EW: Explaining why |
EWP: Explaining to someone else
(spontaneously) EWT: Explaining to someone else (in response to a teacher or written prompt question) EWS: Explaining to someone else (in response to a non teacher or written prompt question) EWC: Explaining as part of social activity in a community where explaining is a social norm, or part of the community’s emotional orientation. |
|
|
U: Attempting to come to a personal understanding (explaining to oneself) |
UM: Understanding the meaning of something (e.g., a definition) |
UMT: Prompted by a teacher or written prompt UMS: Not prompted by a teacher or written prompt. |
|
UW: Understanding why something is the case (e.g., a theorem and it's proof) |
UWT: Prompted by a teacher or written prompt UWS: Not prompted by a teacher or written prompt. |
Table 1: Revisions to the model based on work at the
grade 10 site.
While some research has been done in classrooms on the development of students’ reasoning, none has specifically addressed the issue of the development of deductive reasoning at both the primary and secondary levels or the role of students’ needs in this development. Furthermore, much of the research that has focused on deductive reasoning is not directly applicable to contemporary Canadian schools as it has been done in contexts far removed from contemporary
The
Psychology of Students' Reasoning in School Mathematics
David A Reid
Page I-8
To Beginning of Section | To End of Section
Canadian
classrooms, and has employed models of deductive reasoning that neglect needs
for reasoning.
One example is Fawcett’s (1938) research which analysed the development
of students’ reasoning in geometry and in real world situations during an
experimental full year course in Euclidean geometry. While many of Fawcett’s experimental methods are still
useful, the curricular shift away from Euclidean geometry means that his
findings are no longer directly applicable.
Balacheff, Arsac, Mante, and others (Arsac, Balacheff, & Mante,
1992; Arsac, Chapiron, Colonna, Germain, Guichard, & Mante, 1992) engaged
in classroom research in France in which the development of mathematical
reasoning was observed in the course of a unit on mathematical proof that is
first introduced in the equivalent of grade 7.
As Canadian curricula do not provide such opportunities to focus
directly on mathematical reasoning, this research is also not directly
applicable, however some of the methods used by these researchers are.
Some research employing methods similar to those of the PRISM project has
been done in primary schools. Teacher/researchers
have created classroom situations in which deductive reasoning might be
expected to flourish, but their research focus has been on other issues.
Lampert (1990) and Maher and Martino (1996) have conducted classroom research
with grade 5 students on the development of mathematical communication and
community that offers occasional hints at the reasoning of the students
involved. Zack (1995, 1997;
Graves & Zack, 1996) is also engaged in research at the grade 5 level,
focused on children’s construction of mathematical knowledge through problem
solving and joint activity. She
is a collaborator in the PRISM project.
The
Psychology of Students' Reasoning in School Mathematics
David A Reid
Page I-9
To Beginning of Section | To End of Section
Theoretical and methodological background.
The PRISM project derives both its psychological perspective and its
general methodological structure from enactivist theories of cognition, as
described by Maturana and Varela (Maturana & Varela, 1992; Varela,
Thompson & Rosch, 1991). Enactivism
as a theory of cognition acknowledges the importance of the individual in the
construction of a lived world, but emphasizes that the structure of the
individual coemerges with this world in the course of, and as a requirement
for, the continuing inter-action of the individual and the situation.
From this perspective the role of reasoning in mathematics is seen not
as part of mathematics, nor as a result of the students’ needs in a
situation, but as a part of the inter-action between them.
Similarly the data and interpretations of enactivist research are seen
as coming out of the inter-actions between students, teachers, teaching
materials, and the research context. This
approach captures much of the richness of classroom activity, a richness that
is difficult to capture in other ways.
This enactivist style of inquiry (described further in Kieren, Gordon
Calvert, Reid & Simmt, 1996, 1995) has also been described as “brico-logical”
(Reid 1996, 1995a). Brico-logical
research combines the flexibility and creativity of bricolage with an underlying logic of inquiry.
Bricolage, as it is used in conceptualizing brico-logical
research, favours the production of complex structures, theories, models, etc.
appropriate to research on complex systems such as human learners.
The logic of the brico-logical methodology comes from the questions
chosen for research, and the theories and models with which the research
begins. In practice this involves
a continuous and continuing reinterpretation of data from multiple
perspectives that are themselves being continually reinterpreted by the data.
The
Psychology of Students' Reasoning in School Mathematics
David A Reid
Page I-10
To Beginning of Section | To End of Section
In the PRISM project these multiple perspectives are provided both
through the active involvement of a number of researchers, and through the use
of multiple sites for research. The
cooperating teachers, research assistants, collaborator and principal
investigator each bring to the research unique perspectives and goals.
The backgrounds of the teachers and researchers involved are such that
their goals include developing better teaching methods, exploring classroom
social structures, and investigating learning of particular concepts.
The interaction of investigations with different goals and perspectives
allows for the creation of richer research contexts, encouraging the
development of deeper understandings of all the questions brought to the
situation. The presence of
multiple perspectives at each research site corresponds to the presence of the
principal investigator’s perspective at multiple sites.
The same complexity is offered by the multiple data sources in
different classrooms, at different grade levels, over several years.
At the Grade 2 site
data was collected by observing groups of students working with a research
assistant at learning stations. Several
learning stations involving game playing and other mathematical activities
(See Section
II and Appendix
A) were developed to provide
opportunities for students to reason deductively and in other ways.
The children's mathematical activity was video taped and audio taped.
Data was collected primarily with research questions 2 and 3 in mind,
but also for comparison with the existing data from the grade 5 and grade 10
sites. A revised model (produced
in the grade 10 research) was used to analyse the data.
The
Psychology of Students' Reasoning in School Mathematics
David A Reid
Page I-11
To Beginning of Section | To End of Section